题解：CF392B Tower of Hanoi

不妨设 $dp[i][j][k]$ 表示 $i$ 个圆盘从第 $j$ 杆移动到第 $k$ 杆的最小花费。现在要求 $n$ 个在第 $1$ 杆的圆盘移动到第 $3$ 杆上，因此最终的答案就是 $dp[n][1][3]$。

根据一般汉诺塔的移动方法，想要移动 $i$ 个圆盘，就需要先解决顶上 $i - 1$ 个圆盘的移动问题。又因为汉诺塔只有 $3$ 根柱子，所以我们也可以根据这个思路取设计转移方程。假设现在有 $n$ 个圆盘在第 $1$ 杆上，需要移动到 第 $3$ 杆上，因不同的路径的花费不同，所以我们可以先将顶上 $i - 1$ 个盘子移动到第 $2$ 根或第 $3$ 根杆上，计算哪一个花费最小，如图所示：

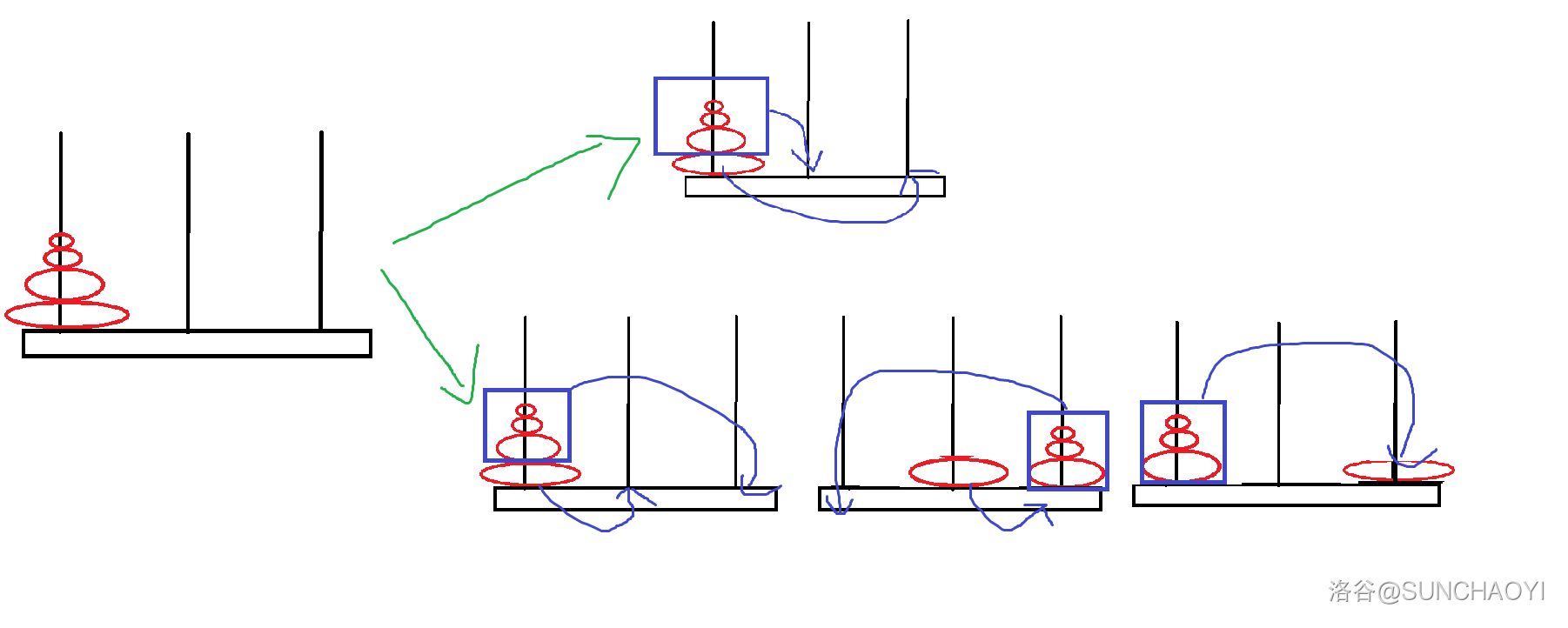
现在设 $dis[i][j]$ 表示将圆盘从杆 $i$ 移动到杆 $j$ 需要花费的金钱数。
根据手绘的垃圾图：

• 第一种移动方式的花费为 $n - 1$ 个盘子从 $1$ 移到 $2$ 的最小花费加上将底部的圆盘从 $1$ 移动到 $2$ 所需的花费，即 $dp[i - 1][1][2] + dis[1][2]$。
• 第一种移动方式分成三部分：
  ① $i - 1$ 个盘子从 $1$ 移到 $3$，底部的圆盘从 $1$ 移动到 $2$；
  ② $i - 1$ 个盘子从 $3$ 移到 $1$，底部的圆盘从 $2$ 移动到 $3$；
  ③ $i - 1$ 个盘子从 $1$ 移到 $3$。
  把所有的花费合并起来就是：$dp[i - 1][1][3] + dis[1][2] + dp[i - 1][3][1] + dis[2][3] + dp[i - 1][1][3]$。

最后，我们把这两种不同的花费取最小值就是 $dp[i][j][k]$ 的答案。总结一下，转移方程就是：$dp[i][j][k] = \min (dp[i - 1][j][l] + dp[i - 1][l][k] + dis[j][k],dp[i - 1][j][k] + dis[j][l] + dp[i - 1][k][j] + dis[l][k] + dp[i - 1][j][k]) (j\neq k)$。($l$ 想必就是中间的一个媒介盘了)

有了转移方程，代码也就好写了，时间复杂度为 $O(n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#include <iostream>
#include <cstdio>
#define ll long long
#define l 6-j-k
using namespace std;
const int MAX = 45;
ll dis[4][4],dp[MAX][4][4];
int main ()
{
    //dp[i][j][k] i 个盘子从 j 移动到 k 的最小成本
    int n;
    for (int i = 1;i <= 3;++i)
        for (int j = 1;j <= 3;++j) scanf ("%lld",&dis[i][j]);
    scanf ("%d",&n);
    for (int i = 1;i <= n;++i)
    {
        for (int j = 1;j <= 3;++j)
        {
            for (int k = 1;k <= 3;++k)
            {
                if (j == k) continue;
                ll da = dp[i - 1][j][l] + dp[i - 1][l][k] + dis[j][k];//移最顶上的2个到中间 
                ll db = dp[i - 1][j][k] + dis[j][l] + dp[i - 1][k][j] + dis[l][k] + dp[i - 1][j][k];//移最顶上的2个到第3根 
                dp[i][j][k] = min (da,db); 
            }
        }
    }
    printf ("%lld\n",dp[n][1][3]);
    return 0;
}