题解：B3600 [图论与代数结构 101] 图的代数表示

Update on 2021.07.10：修改了题解中关联矩阵【无权图】 部分的错误。

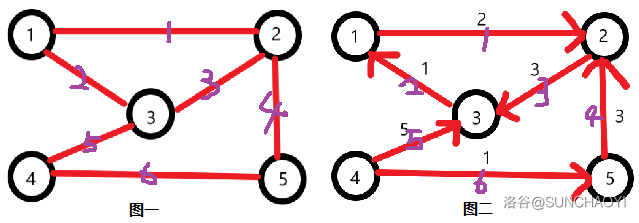
这道题目需要极大的耐心以及细心程度，但是思维难度不大，按照题意模拟即可。【注：本题解所有内容涉及的图片见文章底部。图片的圈中的黑色数字为结点编号，边上的紫色数字为边编号，边上的黑色数字为边权。】

前置

设输入的一条边为 $(u,v)$，$dis[u][v]$ 为非零时即有连边。

判断重边：if (dis[u][v]) chong = 1;//dis非零，说明出现重边；
判断自环：if (u == v) itself = 1;//说明是自环。

邻接矩阵【无权图】

邻接矩阵表示结点之间的邻接关系。该矩阵是由 $n \times n$ 的布尔数组组成，若 $G[i,j] = 1$，则表示一条 $i$ 至 $j$ 的边；若 $G[i,j] = 0$，则表示没有一条 $i$ 至 $j$ 的边。因此不难发现，在无向图的邻接矩阵中，有 $G[i,j] = G[j,i]$。

特点：可以表示自环，但无法表示重边。

如图一，这是一张结点数为 $5$ 的无向无权图，将其表示成邻接矩阵为：

$\left [ \begin{matrix} 0&1&1&0&0\\ 1&0&1&0&1\\ 1&1&0&1&0\\ 0&0&1&0&1\\ 0&1&0&1&0\\ \end{matrix} \right ]$

因此可以得到代码：

if (!ty_2)
{
  int u = read (),v = read ();
  if (!ty_1) dis[u][v] = dis[v][u] = 1;//无向图
  else dis[u][v] = 1;//有向图
}
for (int i = 1;i <= n;++i)//矩阵的打印
{
    for (int j = 1;j <= n;++j) printf ("%d ",dis[i][j]);
   puts ("");
}

权矩阵【赋权图】

与邻接矩阵相似，表示结点之间的邻接关系。该矩阵是由 $n \times n$ 的数组组成，若 $G[i,j] = d$，则表示一条 $i$ 至 $j$ 的权值为 $d$ 的边；若 $G[i,j] = 0$，则表示没有一条 $i$ 至 $j$ 的边。

特点：可以表示自环，但无法表示重边。

如图二，这是一张结点数为 $5$ 的有向赋权图，将其表示成权矩阵为：

$\left [ \begin{matrix} 0&2&0&0&0\\ 0&0&3&0&0\\ 1&0&0&0&0\\ 0&0&5&0&1\\ 0&3&0&0&0\\ \end{matrix} \right ]$

代码与邻接矩阵大题相似，无非把 dis[u][v] = 1 改为 dis[u][v] = d，故不再赘述。

关联矩阵【无权图】

关联矩阵表示结点与边之间的关联关系。该矩阵是由 $n \times m$ 的数组组成，设矩阵为 $G$，则有 $\forall x \in G,x \in \{1,0,-1\}$。对于无向图，若 $G[i,j] = 1$，则点 $i$ 是边 $j$ 的端点；对于有向图来说，若 $G[i,j] = 1$，则点 $i$ 是边 $j$ 的始点，若 $G[i,j] = -1$，则点 $i$ 是边 $j$ 的终点。若 $G[i.j] = 0$，则点 $i$ 与边 $j$ 不相连。

特点：可以表示重边，但无法表示自环。

如图一，这是一张结点数为 $5$ 的无向无权图，将其表示成关联矩阵为：

$\left [ \begin{matrix} 1&1&0&0&0&0\\ 1&0&1&1&0&0\\ 0&1&1&0&1&0\\ 0&0&0&0&1&1\\ 0&0&0&1&0&1\\ \end{matrix} \right ]$

代码如下：

int u = read (),v = read ();
if (!ty_1) con[u][i] = con[v][i] = 1;//无向图
else con[u][i] = 1,con[v][i] = -1;//有向图一个为始点，一个为终点
for (int i = 1;i <= n;++i)//关联矩阵的打印
{
    for (int j = 1;j <= m;++j) printf ("%d ",con[i][j]);
   puts ("");
}

邻接表

邻接表相当于一张表示结点结构的单链表。对于一张图，结点 $u$ 的表的元素 $v$ 满足 $dis[u][v] > 0$。若为赋权图，则还要记录 $u$ 到 $v$ 的边权。

特点：可以表示重边与自环。

如图二，这是一张结点数为 $5$ 的有向赋权图，将其表示成邻接表为：

因为每个结点的表的元素个数不确定，因此可以用动态数组 vector <int> name[MAX],quan[MAX]。代码很简单：

if (!ty_2)
{
    int u = read (),v = read ();
    if (!ty_1) name[u].push_back (v),name[v].push_back (u);//无向图两个点均加入
    else name[u].push_back (v);//有向图只加单向的
}
else
{
    int u = read (),v = read (),d = read ();
    if (!ty_1) name[u].push_back (v),name[v].push_back (u),quan[u].push_back (d),quan[v].push_back (d);    //此时为赋权图，还需要记录权值
    else name[u].push_back (v),quan[u].push_back (d);//有向图只加单向的
}
//注意，如果某个节点的表的元素个数为 0，也要单独输出一个空行，不能忽略（之前样例有误）
if (!ty_2)//有无赋权的两种情况
{
    for (int i = 1;i <= n;++i)
    {
        for (int j = 0;j < name[i].size ();++j) printf ("%d ",name[i][j]);
        puts ("");
    }
}
else
{
    for (int i = 1;i <= n;++i)
    {
        for (int j = 0;j < name[i].size ();++j) printf ("%d %d ",name[i][j],quan[i][j]);
        puts ("");
    }
}

正向表/逆向表

一种压缩储存的方式，可以节省空间。向量 $A$ 表示结点 $u$ 的直接后继结点在 $B$ 中的首地址(逆向表则为前驱结点)，向量 $B$ 储存结点编号，向量 $C$ 储存权值。

如图二，这是一张结点数为 $5$ 的有向赋权图，将其表示成正向表/逆向表为：

//正向表
1 2 3 4 6 7
2 3 1 3 5 2
2 3 1 5 1 3
//逆向表
1 2 4 6 6 7
3 1 5 2 4 4
1 2 3 3 5 1

设结点 $u$ 的邻接表的元素个数为 $x$。则正向表的三个向量计算如下：对于向量 $A$，首先规定 $A[1] = 1$。对于结点 $1$ 至 $n$，$A[i + 1] = A[i] + x_i$。向量 $B,C$ 便是遍历邻接表中所有元素并记录编号(以及权值)。

代码如下：

for (int i = 1;i <= n;++i)//正向表 
    {
        zheng.push_back (zheng[zheng.size () - 1] + name[i].size ());//向量 A 的计算
        for (int j = 0;j < name[i].size ();++j)
        {
            zn.push_back (name[i][j]);//向量 B 记录结点编号
            if (ty_2) zq.push_back (quan[i][j]);//向量 C 记录权值
        }
    }