- 坐标 $\texttt{ZJ}$
$\texttt{Day -16 2021.11.04}$
本以为今年没机会了(退役准备,没想到通过今年上半年打的 $\texttt{NOI Online}$ 前 $25\%$ 报名成功了。
$\texttt{Day -14 2021.11.06}$
机房打了套训练赛,分数一般般,因为不是正式比赛,写题时间本来就不多,外加 $\texttt{T2}$ 绕了很久,所以后两题基本骗分,最后 $100 + 100 + 10 + 30 = 240$ 滚粗。
$\texttt{T1}$ 第一眼看以为是 $\texttt{dp}$,稍微想了一下,再瞅了眼数据范围,发现就是道弱智模拟,然后果断用栈切了。(小插曲就是栈不判空,然后一直运行错误……)
$\texttt{T2}$ 一开始没什么思路,直接打了个爆搜外加 $n = 4$ 的特判大概 $40pts$。然后就一直在思考,感觉有规律可循但是又码不出来。想了大概半小时然后和身边大佬交流了一下,发现可以从结果倒退,于是就开始疯狂递归。接下去就是关于字典序的问题,模拟了一下发现因为存在对称性,所以可以边递归边暴力交换。差不多又是半小时码完了,以为自己打了个可能超时的算法,后来才发现又是时间复杂度算错了($\texttt{CSP}$ 惨痛教训),重新计算发现是 $O(2^n \times n)$,那应该就是正解了。
$\texttt{T3}$ 先吐槽一下 $\texttt{SPJ}$ 因为一定要和标准答案一样输出九位小数时才能得分,所以差评差评差评!赛时没啥思路,所以就骗了最简单的一个情况拿了 $10pts$,后来发现有个地方写错了,本来还能再拿(骗) $10pts$ 的。
$\texttt{T4}$ 直接输出了 IMPOSSIBLE,没想到竟然拿了 $30pts$(有 CCF 那味儿了)。
$\texttt{Day -13 2021.11.07}$
补昨天的那套模拟赛。
发现 $\texttt{T3}$ 就是一个 $\texttt{dp}$。有一个前置结论就是将 $p[i]$ 从小到大排序后肯定是去选择一段前缀和一段后缀。设 $f[i][j]/h[i][j]$ 表示选择前/后 $i$ 个同学,有 $j$ 个同学投“好”的概率。对于第 $i$ 位,分类讨论是否投“好”,于是就有转移方程($h[i][j]$ 的同理可知):
当然,初始的条件肯定是 $f[0][0] = h[0][0] = 1$,就是说前 $0$ 位同学肯定没有人会投“好”。最后求答案的时候,因为要平票,也就是说选 $\frac{k}{2}$ 位同学投“好”。再选定 $k$ 个人的时候,前面选 $i$ 位,后面选 $k - i$ 位,然而投“好”的人不确定,所以要通过循环累加答案,最后取最小值。时间复杂度为 $O(n^2)$。
$\texttt{Day -12 2021.11.08}$
继续补模拟赛,但发现还是不会qwq,颓了……复习知识点去了!被初赛的最后一题恶心到了,因此学习一下笛卡尔树。
笛卡尔树是一种二叉树,每一个结点由一个键值二元组 $(k,w)$ 构成。要求 $k$ 满足二叉搜索树的性质,而 $w$ 满足堆的性质。笛卡尔树的中序遍历便是原序列。
保证 $k_i$ 递增,从下往上比较右链结点与当前结点 $u$ 的 $w$,如果找到了一个右链上的结点 $x$ 满足 $x_w < u_w$,就把 $u$ 接到 $x$ 的右儿子上,而 原本 $x$ 的右子树就变成 $u$ 的左子树。每个数最多进出右链一次,可以用单调栈维护,时间复杂度为 $O(n)$。下面放个核心代码:
1 | //k 记录当前的栈顶;top 记录上一次的栈顶 |
$\texttt{Day -11 2021.11.09}$
分治算法专题
- 逆序对
用归并排序模拟过程。假设将有序数组 $A,B$ 合成 $C$,元素个数分别为 $sz_a,sz_b$,指针为 $p_a,p_b$。则当 $A[p_a] > B[p_b]$ 时,$A$ 中 $p_a$ 之后的所有元素与 $B[p_b]$ 形成逆序对,所以答案累加 $sz_b - p_a + 1$。
由于使用归并排序分治求解,所以时间复杂度为 $O(n \log n)$。当然用树状数组的时间复杂度也是一样的。核心代码放一个吧!
1 | while (p1 <= mid || p2 <= r) |
- ST 表
用 $f_{i,j}$ 表示以 $i$ 为起点,区间长度为 $2^j$ 的最值。显然初始化为 $f_{i,0} = a_i$,转移方程为(以最小值为例):$f_{i,j} = \min (f_{i,j - 1},f_{i + 2^{j - 1} + 1,j - 1})$。
在查询区间时,设区间长度为 $k$,则需要找出最大的 $p$ 满足 $2^p \le k$,也就是 $\min (f_{l,p},f_{r - (1 << k) + 1,p})$。时间复杂度依旧是 $O(n \log n)$。
- 平面最近点对
最简单的做法是暴力枚举,时间复杂度为 $O(n^2)$。但是有更优解法,现在考虑分治。
首先将所有点按照 $x$ 坐标排序,并分成左右两侧。利用递归求解左右两侧的最优答案,设为 $(p_1,p_2)$ 和 $(q_1,q_2)$。在合并答案的时候,可能答案在已经被计算完成的同侧,也可能是两侧。
设 $d = \min (dis(p_1,p_2),dis(q_1,q_2))$,显然最优解分布于中轴线两侧时,距离小于 $d$。固定一侧的一个点 $p$,则只需再框出另一侧的 $d \times 2d$ 的区域的点进行答案的更新即可(由数学中的鹊巢原理知最多有 $6$ 个点在该区域中)。
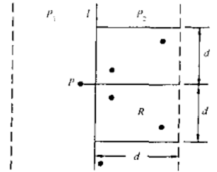
因此,我们将点再按照 $y$ 坐标排序,由于所框的区域单调递增,所以复杂度为 $O(n)$,总复杂度为 $O(n \log ^2 n)$。当然,其中的排序可以用归并排序来代替,在进行合并时,同时进行按照 $y$ 坐标的排序,这样原来用 sort 排序的时间复杂度就被省去,总复杂度降为 $O(n \log n)$。
放个主要代码:
1 | double search (int l,int r) |
【咳咳,话说我竟然被加强加强版的精度卡了好久,没想到最后改成 printf ("%0.0lf\n",ans * ans); 就过了,哭…】
- $\texttt{cdq}$ 分治
这一类问题的特点在于分治划分出来的两个子问题前后具有一定的影响。
由二维偏序引入,$n$ 个有序对 $(a_i,b_i)$,求对于每一个 $(a_i,b_i)$,满足 $a_i > a_j$ 且 $b_i > b_j$ 的有序对 $(a_j,b_j)$ 的个数。该问题的解法就相当于归并排序求顺序对。在排序过程中,可以令 $a_i$ 代表在数组中的位置,$b_i$ 代表值,因此将 $a_i$ 排序之后就能忽略其影响。时间复杂度为 $O(n \log n)$。
而对于三维偏序问题,给定 $n$ 个有序对 $(a,b,c)$,求对于每个 $(a,b c)$,满足 $a_1<a,b_1<b,c_1<c$ 的有序对 $(a_1,b_1,c_1)$ 有多少个。考虑将 $a$ 排序,然后 $b$ 用归并排序,因此现在只需再考虑 $c$ 的大小。
欲求 $[l,p_1)$ 上 $c_i < c_{p_2}$ 的个数,可以用数据结构(如树状数组)维护 $c$ 的值。当选择 $p_1$ 时,加入 $c_{p_1}$ 的值,当选择 $p_2$ 时,直接查询数据结构中小于 $c_{p_2}$ 的数量。注意合并后数据结构的清空,需要倒序删除(若使用树状数组,则需要将 $[l,mid]$ 的所有 $c_i$ 均 $-1$),否则维护的时间复杂度会退化为 $O(n)$。因为使用了时间复杂度为 $O(\log n)$ 的数据结构,再加上之前二维偏序的时间复杂度,因此总时间复杂度变为 $O(n \log^2 n)$。
于是敲了道模板题【模板】三维偏序(陌上花开),放个核心代码:
1 | int main () |
$\texttt{Day -7 2021.11.13}$
前几天一直在学习分治,今天又是周末,所以又是模拟赛。今天的题目感觉比上次还难,其中 $\texttt{T2}$ 数据似乎锅了,所以目前的成绩是:$100 + ? + 0 + 0$。拿到题解发现那题和题解的思路一样,估计数据改了能过,大概 $200$ 分的样子。
$\texttt{T1}$ $5$ 分钟敲完 $O(n^2)$ 暴力,发现竟然可以拿到 $60pts$,尝试去优化算法,但是想了好久都无法降低复杂度。这时候去看了一眼数据范围,发现 $a_i,b_i$ 都为非负整数且 $\sum a_i,\sum b_i \le 5000$,而 $n$ 又巨大,显然数据中最多出现 $5000$ 个非零数。那么只要将非零数单独挑出来,注意记录原下标,这下循环暴力也能解决了。时间复杂度 $O(n + 5000^2)$。
$\texttt{T2}$ 一看数据范围就猜测是 $O(n)$ 的贪心,题目很水,类似求最大连续和的处理,遇到 B 就 ++cnt,遇到 A 就 cnt = max (cnt - 1,0),当然,若出现需要将 A 该为 B 时,就相当于 cnt = max (cnt - 2,0)。由于要求最值,所以尽量修改靠左侧的。如果从 $1$ 开始循环会出错,稍作改变倒序循环就能完美解决。对于 $2^i$ 的处理,一开始用了快速幂,后来发现只需要 $O(n)$ 的预处理就行了。因此总复杂度仍然是 $O(n)$ 的,个人感觉这道题比 $\texttt{T1}$ 简单好多,毕竟是一眼题。
$\texttt{T3}$ 只会打 $O(nq)$ 的大暴力,虽然时限 $3s$,但还是全部超时了。$\texttt{T4}$ 完全不会。
赛后看了题解,后两题还是不太会,可能只能先放着了 qwq。
$\texttt{Day -5 2021.11.15}$
打了考前最后一次的模拟赛,然而一开始就想复杂。明明可以有很好些的 $O(n)$ 优先队列,硬是被打成了 $4KB+$ 的 $O(n \log n)$ 的线段树,还没过大样例,于是乎果断走人……
选择打模拟赛真是个错误。
$\texttt{Day -3 2021.11.17}$
再复习点什么吧……
- 矩阵乘法
$C_{i,j} = \sum_{k = 1}^{M} A_{i,k} \times B_{k,j}$
构造单位矩阵是优化中最重要的部分,以斐波那契数列为例,由于 $f_i = f_{i - 1} + f_{i - 2},f_{i - 1} = f_{i - 1}$,所以单位矩阵为 $\left[ \begin{array}{ccc} 1&1\ 0&1\ \end{array} \right]$。一开始的前两项为$1,1$,所以 $f_{n \mid n > 3} = \left[1 1\right] \times \left[ \begin{array}{ccc} 1&1\ 0&1\ \end{array} \right]^{n - 2}$。还有一个单位矩阵 $I$ 满足 $A \times I = I \times A = A$,则 $I = \left[ \begin{array}{ccc} 1&0\ 0&1\ \end{array} \right]$。
做了道P1707 刷题比赛,然后 $11 \times 11$ 矩阵调了一万年。一开始过不了样例,最后发现矩阵少打了一个 $1$,然后又因为取模 $\texttt{WA}$ 了好几发,最后改成龟速乘才过。
- 单调队列
每个元素最多进队一次,出队一次,因此时间复杂度为 $O(n)$。
还是做了一题P2254 [NOI2005] 瑰丽华尔兹。设 $dp_{i,j}$ 表示滑行到 $(i,j)$ 时的最长距离。而在滑行中因每次只向一个方向滑动,因此可以记录开始移动时与当前的相对位置,并用单调队列维护最大值。当然,滑动需要不碰到家具,则在碰到时清空单调队列即可。这样时间复杂度就降到了 $O(kmn)$。
$\texttt{Day -2 2021.11.18}$
复习数学,看了之前的学习笔记。
敲了一下线性筛,$\texttt{exgcd}$,乘法逆元和欧拉函数的模板。
$\texttt{Day -1 2021.11.19}$
先复习了图论的部分内容,敲了个求割点以及最近公共祖先的模板。然后看了一些 $\texttt{STL}$ 关键字的拼写及 set 的用法。
大概 $19:30$ 离开了机房。
祝愿 $\texttt{rp++}$吧!
$\texttt{Day 0 2021.11.20}$
$7:00$ 起床前往杭师大仓前校区。
$8:00$ 就到了,进去静坐了将近半小时。
开赛后快速看了题,然后感觉 $\texttt{T1}$ 比较好写,和线性筛差不多。写了一遍发现似乎有点问题,筛不出 $14$。然后尝试了一下埃筛,本以为会超时,但是跑了一下大样例发现只要不到 $0.5s$,检查了一下,发现了一个边界的小错误,其它无误后就看了下一题。
至此开始,整个人一直静不下心来,这也就是本场比赛导致失败的重要原因。
$\texttt{T2}$ 看了很久都毫无思路,连 $\texttt{dp}$ 都没有看出来。最后连注释都没删有说明了在考场时的浮躁。
$\texttt{T3}$ 写了一个暴力,但是我在修改多次后竟没发现开了 1e8 的数组,于是乎又没了。
$\texttt{T4}$ 没调完,但是依旧犯了一个致命的错误,就是起点忘记加入到队列当中。
最后洛谷自测 $100 + 0 + 0 + 0 = 100 \texttt{ pts}$,没想到连暴力都挂,心情不佳,怕会影响到 whk,就暂时退役了……
后记
$\texttt{2021 NOIP}$ 结束了,接下去又是一年的漫长训练。一定要吸取教训,多多练习 $\texttt{dp}$,以减少考试时候的紧张感。加油吧!
