目录

【省流版】
I 题是正解却被卡常的，H 是比赛结束后 2s 以后过的……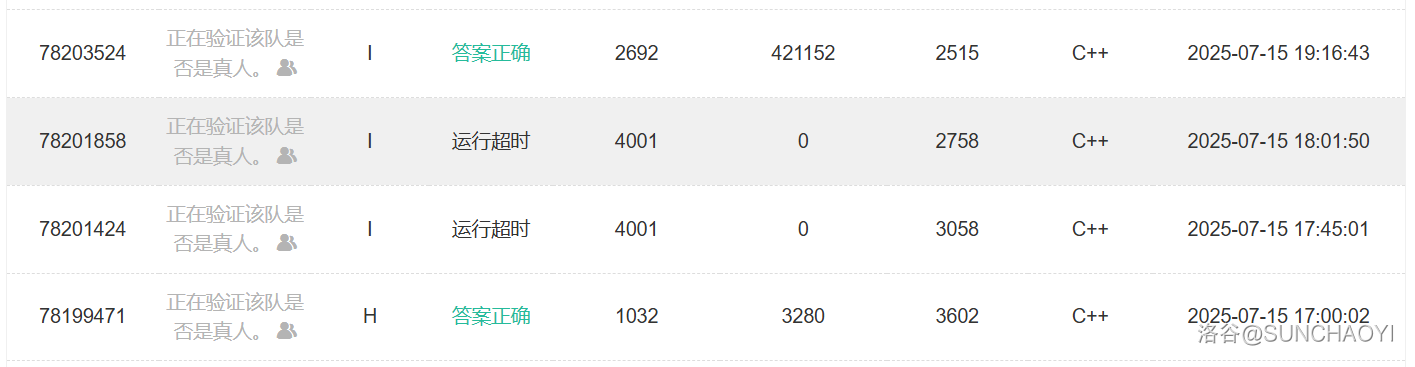


【Zlw】上来先开始看 E，看到平方差想到化成 $(a+b)(a-b)$ ，但是一开始以为是质数不合法。不过后面细想一下发现分奇偶考虑，$(a+b),(a-b)$ 奇偶性要相同，然后就能得到答案了。

【Scy】G 题题意有点迷惑，看了一遍仍然没懂，于是让 zlw 先开始敲题，趁着他卡住了一下的间隙签到完毕。

【*】前两题在 16/18 min 的时候通过。

【Zlw】接着开了 L。发现满足条件的 $a_i$ 大致是小于中位数。稍微细想可以发现是严格小于 $a_{中位+1}$ 。于是套点数据结构就可以单 $\log$ 了，不过一开始没想离散树状数组被孙✌怒骂一通，后面想想虽然离散化麻烦总归没有平衡树麻烦。还好写了离散化，据说平衡树被卡常了。

【*】但是 L 爆 int 没有发现浪费了一点时间，1h 多一点 $-1$ 通过 L，之后 zlw 和 sky 看了 K 题，scy 开始 D。D 题应该是想到第一步大与根号的质数幂次为 $1$，但是发现不太会高级筛法，加上看榜提交数量过百但无人通过，于是放弃了这题。大概空机了 15 min，sky 说大致会 K，于是开始写。

【Sky】题目大意就是有一个节点数为 $n$ 的无向图，但每个点的度数最大为 $3$，而且给定了遍历图时的走法，可以理解为固定路线。要求从节点 $i$ 出发能走到的最多边数。

一开始我理解为线路可能是链加环的形式，想了半天怎么做这个记忆化搜索，但经过讨论后发现任何一个线路都一定是环，因为题目给了“所有走廊都是双向的，因此如果从房间 $u$ 到房间 $u$ 有一扇门，那么从房间 $v$ 到房间 $u$ 也有一扇门”，然后就好做很多了，只需要遍历这个固定路线，发现环之后把环上的所有点的这个路线状态都更新答案为环的边的数量即可，然后记忆化，总复杂度 $O(n)$。

这个路线状态可以理解为，点 $u$ 向它的某个节点的边，因为同一个点可能在不同的线路环里，但是一个边一定只被一个环包含。

【*】这道题似乎走弯路走的挺久，写了将近两小时，还 TLE 了一发。Sky 在写这题的时候 Scy 和 Zlw 讨论了一下 H，然后 Scy 独自开了 I 并认为得到了正解，并和 zlw 进行了两次确认。Sky 在写了 1.5 h 的时候遇到问题才进一步和我们讨论，再发现特殊性质以后 20 min 不到通过了这题。感觉这题耗时过久的原因出在前期考虑不充足，然后遇到问题没有即时的讨论。不过好在仍然有多线作战。

【Scy】过了 3 h 的时候开始写 I，差不多 40 min 写完，一个 $O(n^3 \log n)$ 的区间 dp 加上二分优化。但是提交在 4s 时限的情况下依旧超时，意识到被卡常后和队友交流尝试多次修改，但是无果，折腾了快一个小时仍然没有通过。

【*】 I 这个卡常实在是有点无语（一方面可能牛客的评测机确实有点慢了，第一发提交测了好几分钟才返回 TLE，估计也是靠后的几个点）。赛后随便乱改，删掉了一个 $O(n)$ 的循环反而过了（$n = 420$）。

【Zlw】H 是很快就有人通过的题，但是据说首发是暴力干过去的。

第一眼看没读懂题，孙✌中译中了一下仍然不是很懂，最终花费大量时间看完题目。然后孙✌提出了可以按照连续相等的段，然后计算 $\sum \binom{|s|}{2}$ 的方式得到结果。结合奇特的时间复杂度要求想到了 bitset，但是发现要手写，没写过，遂抄板子。

还得把 unsigned long long 分成 $4$ 段处理，看着很复杂，遂没敢写。队友写题的时候想了一下，发现 $1$ 操作可以将差分操作延迟处理，然后处理 $[0,65535]$ 每个数做前缀和之后的结果，以及前后缀 $0$ 个数、中间的对答案的贡献，然后根据上述说的每个 ull 拆成 $4$ 份合并。最后 1h 开写，挂了一点点，查出错再交，又删了一会调试，赛后 2s 过题QAQ。

【*】说实在 I 的卡常确实有点红温了，还时不时地抢了 Zlw 的机位，导致他最后几分钟才开始提交，然后发现错误的时候是 59 分，删完注释提交发现已经 too late 了。


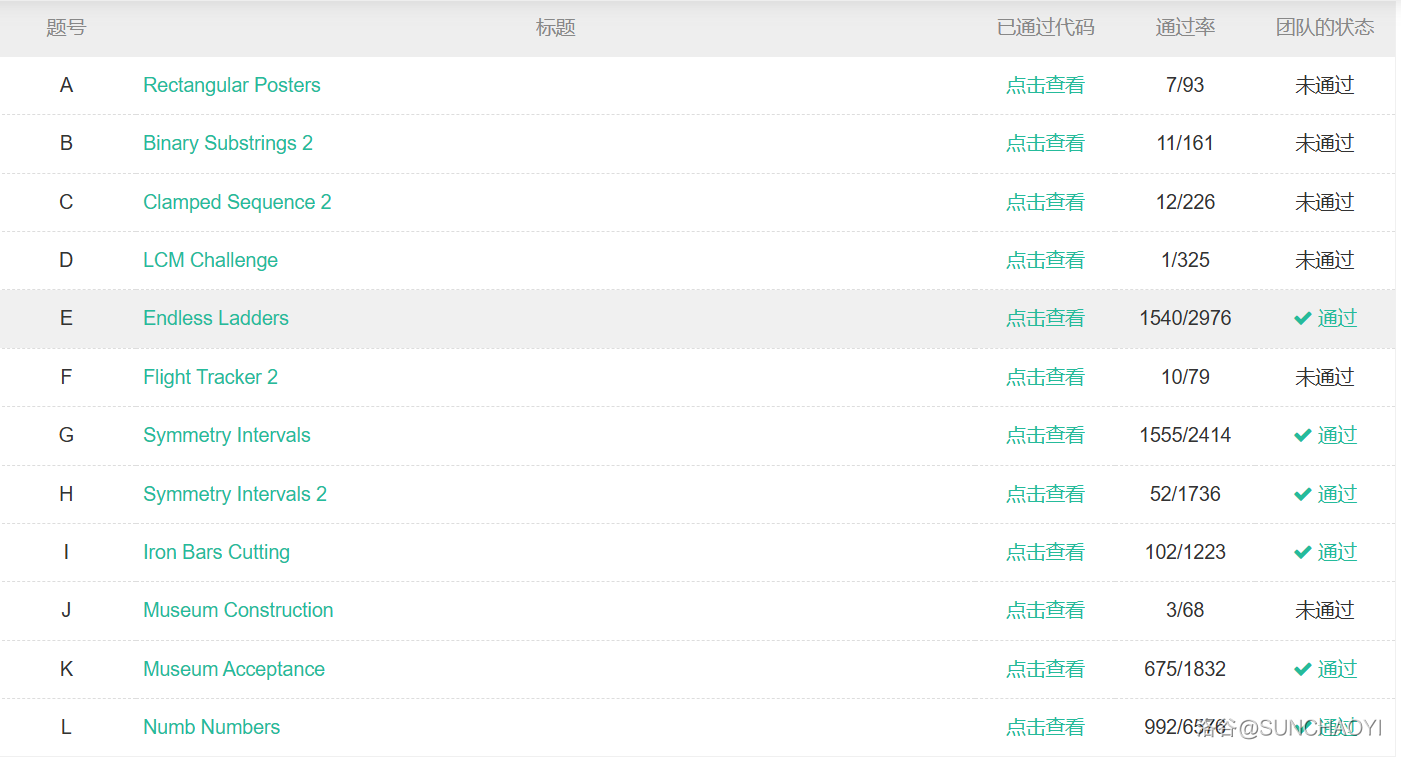
【Scy】看题解的时候才发现 B 是和 H,I 一个难度的，是构造题，我可能会更擅长这一类题目，可以由于赛时通过人数不多，并未发现这道题目。

【省流版】孙老板在第一次赛后复盘时有言：对你们来说目前合适的 timeline 是：$\texttt{1h}$ $3$ 题，$\texttt{3h}$ $5$ 题，$\texttt{5h}$ 保 $6$ 冲 $7$。 于是乎：

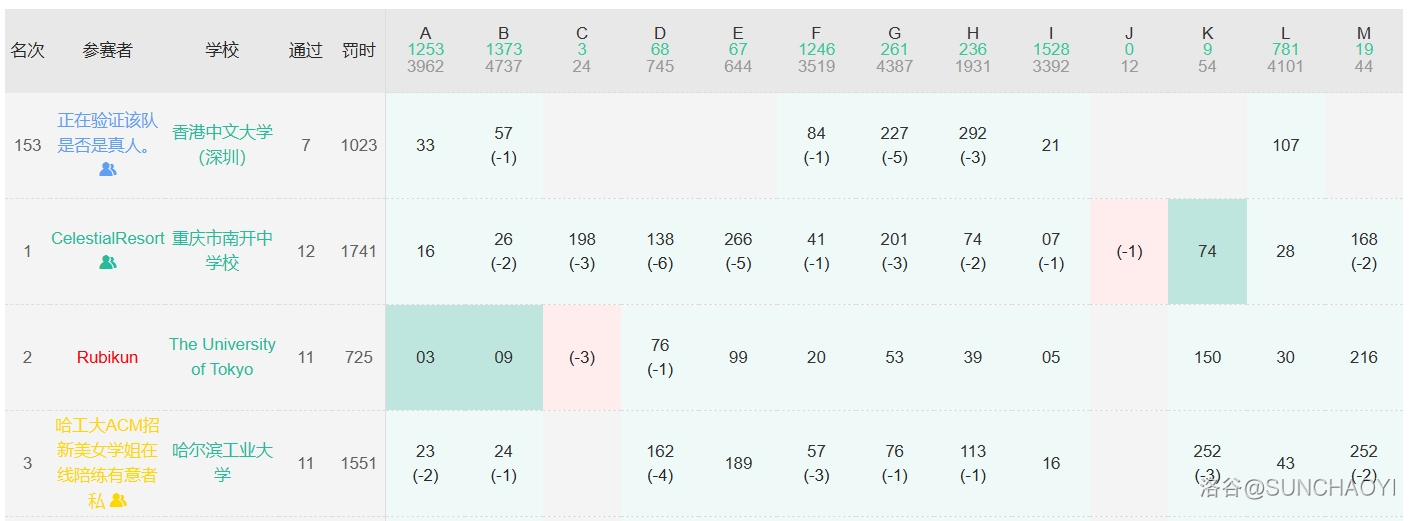
在 $4:52$ 时通过 $7$ 题并下班，与预言完美的契合起来！（所以说孙老板说我们能 AK，是不是就能 AK 呢）

【Zlw & Sky & Scy】Zlw 一开始在看 A，Scy 和 Sky 在讨论 I，但是 Zlw 没怎么读懂 A 题，于是加入了 I 的讨论。I 确实是签到，但（由于 Scy 还在煮水饺吃）稍稍想歪了一点，想要开始大力分类讨论。Sky 一开始考虑变形 $(x-y) \bmod k = (k \bmod y) - (k \bmod x)$，发现 $k=x-y$ 貌似有什么性质。但做了一会之后，Scy 发现直接 $k=1$ 就可以了，快速写，打了个表验证之后就交上去 AC 了。

【Zlw】然后回去看 A，跟 Sky 确认了题意，发现只需要统计 $1$ 的连续段数，被奇特的样例解释卡住了。然后发现是个典型 dp，很快写完。

【Scy & Sky】Zlw 在写 A 的时候 Scy 去看了 B。吸取了上一次的教训，等 Zlw 开始上机的时候拉来 Sky 确认了做法。如果能找到 $a_i > a_i \oplus a_j$
或者是 $a_j > a_i \oplus a_j$ ，就能满足这个不等式。然后 Sky 发现一种很简单的例子就是 $a_i$ 和 $a_j$ 有着相同的最高位的时候，也就是 $2^k \leq a_i, a_j < 2^{k+1}$ 一定是能满足这个不等式的。Scy 进一步发现这道题非常诈骗，根据鹊巢原理 $n > 64$ 的时候都是 No，其余暴力。写完直接交了，结果 WA。。Zlw 在切了 A 之后来看这道题，怒喷 Scy 这个 fw， $a_i \le 10^{18}$ 还在用位运算模拟（坏了被 $a_i$ 的二进制和 $2^{a_i}$ 搞晕了）。于是 Zlw 提出了不等式 $2^x \leq 2^x+2^y \leq 2^{x+1} (x\geq y)$ 又因为 $x \oplus y$ 一定是整数，即要么小于等于 $x$，要么大于等于 $x+1$，我们可以这样子把底数 $2$ 直接消掉，进而比较 $x$ 和 $x \oplus y$ 即可便在 $00:57$ 的时候通过了这题。

【Zlw】然后去看 F。但是看错题了，没看到“只能操作一次”，Scy 读完题发现只能操作一次，然后一起讨论发现直接贪心选择最大的 $0$ 连续段即可。剩下的也可以只用一个 $f$(连续段长度)去表示，不用写特别多的模拟，浪费了很多时间在读题上。

【*】F 写完以后 WA 了一发，原因是 vector 为空的时候没有做保护措施，仍然会有取里面元素的情况。Zlw 写完以后 Scy 大致测了几个额外的样例，但是没有太注意到这种 corner case。

【*】Zlw 写 F 的时候，Scy 去看了计算几何 G，Sky 看了图论 L。

【Zlw & Sky】这道题题意比较复杂，但其实就是一个简单的计数问题。一开始没注意到全是环，中间出现了反复横跳的确认。再细读了题目的 Input 保证如果 $i \neq j$，则 $a_i \neq a_j$，然后题目又说了每个人一定爱着一个人，不管是自己还是别人之后，终于确定了这个关系一定是由几个分开的环组成的（包括自环）。

确定之后就是简单的分环的节点数量的奇偶性讨论就好了，实际上只有两种大情况：

  1. 有两个奇数大小的环，那么被禁止结婚的人一定在这两个奇数环里面，这两个对方案数的贡献就是两个环大小直接相乘。

  2. 全是偶数大小的环，那么两个被禁止结婚的人一定在同一个环里，分环节点的奇偶位置稍微讨论一下就好了。

对于普通的偶数环，$\lvert V \rvert = 2$ 的时候贡献为 $1$，$\lvert V \rvert \geq 4$ 的时候做的贡献为$2$。最后把这几个贡献乘起来就好了。如果出现了不是上面两种情况的，直接输出 $0$。跟 Zlw 确认了一下之后，Zlw 就直接写了，很快A C。

【Scy】 $01:50$ 他俩写完 L，我赶紧找来 Sky 讲了一遍我的做法。分类讨论点在多边形内还是外。在外面答案恒为 $2\pi$，在内部答案为距离最远点之间的最大角度。Sky 验证了我的做法，于是开写。很快写完后提交，WA。Sky 给我提供了几个 hack 数据，发现写挂了点的地方，改完以后仍然 WA。于是开始红温，后来想到可能是精度的问题，从 acos() 搭配叉乘算角度改为直接用 atan2()，但是又由于忘记变换了参考系，一共 WA 了 $5$ 发，于 $03:47$ 时候通过。

【Sky】Zlw 在写 L 的时候，Scy 找我来做这道计算几何，我当时就有种不好的预感，但这道题确实是下一道该做的了，也没办法。这题的正解实际上就想了不到十分钟，但是因为它是计算几何，加上 $10^9$ 的数据范围，不出意外，被卡精度了。被卡了一个多小时，中间还一度怀疑做法是不是有问题，最后在这个做法上优化了一下精度问题，终于 AC 了。

【*】Scy 在静态调试的时候，Zlw 又和 Sky 讨论出了 H。但是写完提交了几次都是 WA，也在红温的边缘（尤其是 Sky，连续看了两坨）。G 计算几何的通过算是稳定了队内的情绪。

【Zlw】Scy 写 G 的时候我和 Sky 讨论了一下，发现枚举边作为路径上最大的 $w$，然后问题就转换为若干个一次函数在某个位置的最优解。但是这里想的双指针做法假了，一直到最后 40min 才发现。然后 Scy 调出了 G，来一起想，因为没人会改李超树的模板，提出是否可以维护一个上凸包。观察规律尝试了一个形似单调栈的东西维护上凸包过了。

【Sky】在红温 G 的时候，我也来帮 Zlw 想了下 H，他说了下他的做法，但我当时其实只听懂了前半段，后半段有点迷糊没有听懂，就认为 Zlw 这个做法没有任何问题，在思考 G 错在哪的同时，Zlw 上机直接敲了 H。

但问题刚好就出在这个后半段，在处理 $t_j - w_j \times k_i$ 这个式子的时候，Zlw 的双指针神秘做法其实是有问题的，最后快半个小时的时候突然发现。然后想着这里好像有点像李超线段树，但这道题的通过人数应该用不到这么复杂的数据结构，三个人就同时开始想怎么去解决这个问题。最后两个队友想到了单调栈维护下凸包，Zlw 在高压之下光速写完并一发过，激动人心啊，激动人心。

【*】H 的做法假了一小部分，说明验证正确性这一部分仍然需要改进。好在大家不断地相互鼓励下，提出了凸包的优化，在并不是那么熟悉的情况下在 $04:53$ 极限通过了 H（也算是上一次赛后两秒过题的补偿了吧）！

【省流版】似乎还是简单场，$7/11$ 题，$\texttt{rank 181/1610}$。$7 \to 8$ 题的 gap 似乎挺大的，四小时做完 $7$ 题以后就开始坐牢，最后提前下班。

【*】Zlw 在考 STA2001，所以晚了点来；然后 Sky 要去上暑课，所以提前两小时走了；只有 Scy 全程在吃 【数据删除】。

【Scy】看到了 F 是签到，2 min 一发通过。Zlw 在路上瞅了眼 D，大致确定了一个结论，于是丢给我来实现，在 $00:15$ 通过。

【Sky】J 也是签到题，考虑直接暴力的复杂度很低，大概是 $O(t\log V)$，但我写太丑了，导致T掉两发（想割手.jpg），想了一下好像有结论，就是先同除以 $\gcd(a,b)$ 使得互质，然后如果有 $a+b=2^k$，答案就是整数 $k$，否则无解，过题了。

【Scy】在 Sky 红温的时候去看了 A，是一个构造，确实是我的题，于是就开想。想到一个稍微有点奇怪但是好写的构造方法，用 set 在维护。之后又和 Zlw 看了 E，大概确认了他的做法。

【Zlw】等 Sky 红温完毕以后开写，看到这个 $\div \times d$ 的形式想到可以看质因数，然后统一每个质数的个数。然后一开始忽略了 $\times$ 操作，以为是之前的经典结论挑两个不同的数 $-1$ 减到 $0$，犹豫了较长时间才发现可以 $\times$，于是只跟奇偶性有关了。然后分 $n$ 的奇偶和质数的奇偶讨论。但是筛的时候发现 $O(m \log m)$ 预处理需要 $2s$ 卡线超时，发现筛的有点丑，想办法优化，然后用线性筛处理出最小质因数然后直接用类似 dp 转移的方式继承上一位出现次数为奇数的质因数。预处理时间降到 1s，但第一次交上去 WA。想了一会儿发现 $n = 2$ 时候需要特判，修改了下后过了。据说题解是 $O(m)$ 的哈希做法。

【Scy】写了一发然后 WA，于是敲了一个 checker 看了半天一直拍不出错，于是重新读题，发现是一行一列的 $\operatorname{mex}$，而我写的是行列加起来的 $\operatorname{mex}$。于是复制了一遍我的代码以后再次提交，终于通过。

【Zlw & Sky】H 题与 Sky 讨论发现可以维护一个点的最短到达时间，然后直接判断。细想了一会发现可以直接染色标时间戳，这个时候 Scy 在上机，然后细节还挺多的，遂与 Sky 反复确认细节。最后写的是染色 $+$ 倍增使得复杂度为 $O(n \log n)$，Zlw 强大的码力很快写完一发过。

【Zlw】B 上来想到一个需要 $3\log$ 的构造，可以把 $b$ 消成 $0$，$a$ 变成 $c$，然后 $b \rm xor a$，在把 $b$ 变成 $0$ 的过程中用最高位对 $a$ 进行 $\rm xor$ 操作。但是发现当 $\max(a,b) < c$ 时很难办，乘上去的 $30$ 次操作难以避免，但是联想到 $b$ 消成 $0$ 的”顺路”属性，想到能不能“顺路”改变 $a$ 的更高位。然后又从 $a=0,b=1$ 的情况想到可以 $\times 2+1$ 的形式凑出更高位，于是将两个想法结合，发现可以平移 $c$ 的较高位与 $a$ 对齐，然后用 $b$ 改造较高位，用 $b=1$ 凑出较低位，发现次数刚好够，测试了一下极限大概在 $63$，于是交题通过。

【Scy】坏了 B 也是构造，但是被 Zlw✌给秒了。难点主要是 $\max(a,b) < c$ 的时候，还在想各种奇怪的方法的时候 Zlw 丢给我一个图，我确认了他的做法，然后他开共享屏幕写，$03:49$ 通过该题。

之后我尝试看 I，是一道纯数学题，先去学了一下置换群才勉强看懂题目。用 OEIS 大致弄出了点结论，猜测是个多项式工程，但是有一些板子并不会写，遂下班。

【Sky】今天比较摆，两位队友过题很快，而且因为后面要上暑课，所以只打了前三个小时😭，逐被带飞。

【省流版】被 Zlw 和 Sky 带飞，Scy 被构造硬控，硬是吃了坨大的。$4/13$ 题，$\texttt{rank 88/1544}$。

【Scy】这场有难度，上来一下子没有发现很签到的题。过了几分钟看 F 有人过题，遂看题。第一眼是 dp，想了一下发现交换的代价显然是可以撤销的，于是直接按照交换到第一位的代价从大到小排序，然后贪心选即可，$00:19$ 一发通过。

【Zlw】上来先看的 B，一开始过的人比较少，有点不太敢确定做法。简单和 Sky 确认了一下，等 Scy 写完以后我上手写 B，的确就是维护一个“死胡同点“最右边到达的列数即可。

【Scy】发现 D 是一个和线性代数有关的构造，Sky 手玩了一会儿毫无想法，而 Zlw 自然不去碰构造的，于是我开始想题。

【Zlw & Sky】 Sky 先看了一会，尝试从多解的结构思考。Zlw 在从 $-1/1$ 转化寻找性质。然后经过 Sky 提醒，发现当两种括号都出现问号时，有很大概率是多解的。从这个角度具体分析，发现如果存在 $\texttt{)(}$ 必然可以通过交换这两位得到多解。进一步研究交换带来的影响，发现即当满足前缀和在 $[l,r)$ 的最小值 $\geq 2$ 时，有多解。且去除掉 $\texttt{)(}$ ，最终必定是形如 $\texttt{(}\cdots \texttt{(()} \cdots \texttt{)}$ 的形式。再观察到每个字符的传输正确概率是 $\frac{1}{2}$，最后概率分母为 $2^{\lvert s \rvert}$，然后 Zlw 提出分子可以考虑计数，固定一个左括号，然后去计算右边有哪些右括号可以变成 $\texttt{?}$。Zlw 佬确认做法之后很快就过题了。

【Scy】纸笔迷题中。一开始考虑的是 $n \times n$ 的 01 矩阵行列式的最大值。$n = 3$ 行列式为 $2$，一个显然的构造如下：

然后之后进一步尝试，发现 $n = 4,5,6,7$ 时最大为 $3,5,9,32$，其实也就是这个数列。大概找到了构造最大值的方式，但是发现由最大值不太好调整到任意值，于是倒闭。

【Sky & Zlw】简化版的推箱子问题，没有小人，箱子可以自己动，所以变得挺简单。因为没有限制箱子对应的目标，所以观察得知，只要一个连通块的箱子数跟目标数相等就一定有解。

Sky 提出箱子可以互相”穿墙“，具体表现为通过”继承“的方式让整体看上去像是穿过去，由此发现窄道并不会影响答案，于是直接判连通块内箱子数等于目标数。（当一个箱子挡住另一个箱子去路时，可以两个都往前走一格，做到一种“穿过”的效果，因为箱子之间没有区别，所以合法）。而且这样子做使得答案特别容易构造，找到一个箱子对应随便一个目标的移动路径（Sky 取了最短路），如果有箱子挡住就对移动路径做一次 reverse 操作，然后直接输出即可，很巧妙。

跟 Zlw 讨论确认算法简单之后我就上机写了，但是大模拟码量比较大，我写了很久，码力这一块还得练。而且因为一个唐问题（bfs 计数同一个连通块内的箱子和目标数居然算重了很多）WA 了几发，导致做了快两个小时。还好这题做出来的人也不多，排名提升了些。

【Scy】还在纸笔迷题中。想来想去还是回到二进制拆分上。基于 $n = 3$ 的构造外加对角矩阵可以使得 $|A^{\prime}| = |A| \times 2$，然后再第一行放一个 $1$ 可以实现 $+1$ 的效果。啊，被硬控 4h 终于是想到解法了，但是实现有一定细节，留给我 15 min 去实现。

写完以后没有测直接交，但是 WA。简单修改了一下，再交，已经是 $04:59$，评测队列超级长，等返回 WA 的时候已经结束了。

害，被一道构造硬控了。赛后发现奇偶性有点问题，稍微调整了一下构造就 AC 了。

以后我可以不负责构造了嘛，开点码量题也行（

【Scyの补题】

L 写成表达式为 $x \leftarrow \lceil \frac{x + a_i}{2} \rceil$ 后就可以迭代，注意到区间长度大于 $30$ 时由于 $2^{30} > 10^9$，因此 $x$ 对答案的影响最多差 $1$。于是不超过 $30$ 暴力计算，超过 $30$ 直接用 $x = 0$ 时候的答案（只需要判断是否有 $1$ 的影响即可）。

A 题算是比较逆天，赛时 $16/55$，感觉榜歪到哪去都不知道了。考虑构造三种类型的数（组） $A,B,C$ 作为基，需要满足 $D(A,B) > \frac{1}{2},D(A,C) < \frac{1}{2},D(B,C) = \frac{1}{2}$，这样处理每一行的时候以 $A$ 为基准，需要赢的话就用 $B$，输的话用 $C$。

直接去找比较困难，我直接写了暴力去找。通过程序搜索，发现长度至少为 $3$，值域为 $[0,4]$ 时才有解，以下是我用的一组基：

1
2
3
1 1 2
0 1 3
0 2 2

最后直接按照这个构造即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
if (i == j)
{
    ans[j].push_back (6 * i + 1);
    ans[j].push_back (6 * i + 1);
    ans[j].push_back (6 * i + 2);
}
else if (s[i][j] == '1')
{
    ans[j].push_back (6 * i + 0);
    ans[j].push_back (6 * i + 1);
    ans[j].push_back (6 * i + 3);
}
else
{
    ans[j].push_back (6 * i + 0);
    ans[j].push_back (6 * i + 2);
    ans[j].push_back (6 * i + 2);
}

【省流版】 又是坐牢场，$4/13$ 题，$\texttt{rank 172/1605}$。

【Scy】开局跟榜，I 是签到，分类讨论即可。$n$ 为偶数，直接 $i$ 与 $n - i$ 拼在一行；$n$ 为奇数，$i$ 与 $n - i - 1$ 拼在一行，$n$ 单独成一行。因此答案为 $3n + 1 + [n \bmod 2 = 1]$。

【Scy】 看了 D 构造，打个表找规律，但是没有发现什么有价值的地方。这时候 Zlw 让我来看看 E，读完题以后提出可以按位来算贡献，然后想到了个 DP。由于空机时间比较久了，就没有进一步确认直接开写，他俩去看了别的题目。

设 $f_{i,0/1,0/1}$ 表示考虑二进制下从低往高的第 $i$ 位为 $0/1$ 时，之前位置上 $1$ 出现了偶数/奇数次的数的个数。由于异或，显然第 $i$ 位上的数要奇偶不同，又由于只有从低到高的第奇数个 $1$ 才能有贡献，因此 $f_{i,0,1},f_{i,1,1}$ 与 $f_{i,0,0},f_{i,1,0}$ 这两对数会产生贡献。

1
2
3
4
5
6
for (int j = 1;j <= n;++j) 
{
    ++f[a[j] >> i & 1][st[j]];
    st[j] ^= a[j] >> i & 1;
}
ans += 1ll * (1ll << i) * (f[0][0] * f[1][0] + f[1][1] * f[0][1]);

由于没有确认过做法，在交之前花 5 min 写了个暴力对拍。幸好没有拍出错，提交一遍 AC。

【Sky & Zlw】 E 没思路，Scy 写完签到过来秒了，遂与 Sky 讨论 J。题目大意如下：

给定一个 $\texttt{01}$ 网格，$\texttt{1}$ 每秒向上下左右染色，可以给一个 $\texttt{0}$ 变成 $\texttt{1}$，使得总染色时间最小。

Sky 一开始的想法是取最远点的“中心”，就是找到一个点，距离所有点曼哈顿距离最大值最小。具体来说，先不管这个变成 $\texttt{1}$ 的格子，考虑直接 bfs 模拟一遍染色过程，标出所有格子的最短时间，然后去思考怎么将最大时间那几个格子早点染色。考虑直接取几个最大时间格子的曼哈顿距离中心，即找出一个格子，使得其到几个最大时间格子的曼哈顿距离的最大值最小。即：

其中，$I$ 是坐标范围，$M$ 是最大时间格子的编号集合。

但这样不太好证明正确性，且求取中心需要分 $4$ 个象限分类讨论异常麻烦。而且直接这样做的复杂度是 $O((nm)^2)$，不理想。Zlw 提出可以二分距离，保证正确性，但 Sky 认为太复杂，于是先尝试如何避免分类讨论或者更复杂的操作。然后发现可以镜像翻转把 $4$ 个象限统一到左上角求取。这个时候 Scy 已经写完题，处于空机状态，遂优先正确性写了二分，由于没特判全 $0$ 和数组清空不全 WA 了两发。赛后看群里发现这个 case 也有很多的队伍被卡（会显示用例通过率 $98.78\%$）。

【Scy】A 题看了很久，尝试推了一下式子。$s - t = \sum (k - 2p_i)$，其中 $p_i$ 表示每次选择朝上的硬币的个数。显然 $s - t$ 是奇数且 $k$ 是偶数时无解。又需要满足每次 $p_i \in [s^\prime + k - n,s^\prime]$，其中 $s^\prime$ 为当前朝上硬币的个数。还发现 $n = k$ 时是特殊的，只有 $s + t = n$ 时答案为 $1$，否则无解。但是接下去一直不知道如何处理每次 $p_i$ 的取值，看数据范围很像是结论题，但是找不到规律，没法进一步推进。（坐牢中）

【Zlw】 K 朴素 dp 是 $O(k2^m)$ ，然后尝试了从树形结构出发树形 dp，但仍然非常复杂不确定正确性，且时间复杂度约为 $O(m^2 2^m)$ 不太能够通过。继续观察发现本质不同的链数只有 $O(m^2)$ ，有了一个好写的 $O(m^2 2^m)$ 的写法，因为空机遂写了一下，不负众望的 TLE 了。

【Scy】在 Zlw 的 $O(m^2 2^m)$ 的基础上，我想到可以利用 fwt 和容斥来计算答案，时间复杂度可以优化到 $O(m 2^m)$。这时候需要算组合数，这恰好和题目里的数字在模 $998244353$ 上非 $0$ 对应了起来。Zlw 佬的代码和我的代码不太能兼容，于是直接重写。

直接选择利用 dfs 树的性质来求出一条路径是否经过第 $i$ 条关键边（这里需要注意是用深度大的结点去判断！！当时这里还调试了很久），然后直接放到状态里，进行 sosdp，得到 $g_S$，表示状态为 $S$ 的子集的路径条数。然后枚举答案，尝试用 $i$ 条边去覆盖这 $m$ 个关键点。用容斥就能算出答案，即 $tot = \sum \limits _{i = 0}^{2^m - 1} (-1) ^ {[(m - \operatorname{popcount}(i)) \bmod 2 = 1]} \times \binom {g_i}{i}$。找到第一个使 $tot$ 非零的 $i$ 就可以直接输出，否则无解。紧赶慢赶终于在 $04:45$ 的时候通过。

【Scy】最终 $4$ 题遗憾离场了。不过好像排名还行，还是上分了！

【Sky】今天这场很史，我也很摸，被队友带飞😭。

【省流版】开局签不上到，榜歪得很，导致最后没来得及过 $B$。$5/13$ 题，$\texttt{rank 156/1437}$。

【Scy】开局看 C，$f(p)$ 是好求的，就是第一类斯特林数，但是三次方没想法，打了表也没发现什么规律。但这时候 Zlw 的 K 有了想法，于是先让他来写。

【Zlw】其实一开始看的就是 M 这道题，并且很快的跟 Sky 讨论出正解。但是并没有严格的证明正确性且当时没人过，于是看其它签到题去了。$n$ 为奇数时容易构造，为偶数时需要找到最相近的两个数填到最高位，剩下的构造方案固定。理论上只要找到最优的最高位即可。当时发现可以找到最靠近中心的最优最高位，然后直接确定或者进行一次 $O(n)$ 的比较。但是经过一系列莫名奇妙的操作和严重歪掉的榜，我们忘记了这道题。

【Zlw】K 看到整体加再取 $\gcd$，想到经典差分，变成了取前后缀原数组以及中间差分数组的 $\gcd$。

然后又想到经典前/后缀 $\gcd$ 变换次数为 $O(\log)$ ，于是暴力枚举前后缀不同值，贪心选取使中间区间最小的情况，再配一个st表查询即可。这部分复杂度 $O(\log^2 w)$ 完全可以接受。

【Scy & Sky】Scy 和 Sky 找规律，提出了一个 $f_{i+1,j}=f_{i,j}\times i+f_{i,j-1}$，然后 Zlw 设 $f_i$ 的 $\rm OGF$ 为$F_{i}$，$F_{i+1}=xF_{i}+iF_i=(x+i)F_{i}$，发现$F_n=\prod_{i=1}^{n-1}(x+i)$，于是鼓励 Scy 用分治+ FFT 但并未被采纳（想🍑）。

【Zlw & Sky】
L 题的题目大意是给定 $m$ 个区间，求长为 $2n$ 的字典序最小的合法括号串，满足每个区间内至少有一个左括号。若无解，则输出 $-1$。

考虑没有约束的话，字典序最小就是 $\texttt{(((…)))}$ 这样的形式，然后先把有包含的区间删掉大的，再根据区间从右往左贪心，把每个区间最左边的右括号换成左括号。

构造/贪心题 Zlw 不太擅长，但是 Scy 在写忙，场上此时看起来也只有这题可做。在 Sky 的帮助下慢慢确定了交换最右侧左括号的策略。但是细节比较多，写挂了，WA 了好几次。这个时候有点红温，大概能确定是 WA 在交换括号的细节上了。后面想了想，可以先贪心的填必填的左括号，再补全剩下的就可以。重构了一下过了。

【Scy】我按照 Zlw 给的多项式的想法，就是 $f(x) = x(x + 1)\cdots(x + n)$ 的系数就是具体的答案，然后按照这个式子出发，$F(x) = x \times (x^k)^\prime = kx^k$，因此 $F^3(x)$ 可以把 $k^3$ 的系数搞出来。之后经过一系列复杂的求导之后，大概过了 2h 才通过此题。

*赛后看题解以后的做法：

设 $I_i$ 表示元素 $i$ 是否在栈内，也就是

把立方看成选三个项相乘，于是有

考虑单个元素 $i$ 在栈中，则 $1 \sim i - 1$ 需要在 $i$ 前面，共 $(i - 1)!$ 种，而 $i + 1 \sim n$ 随意放置，共 $\frac{n!}{i!}$ 种，因此共有 $\frac{n!}{i}$ 种。同理得到双元素和三元素的方案数为 $\frac{n!}{ij}$ 与 $\frac{n!}{ijk}$。预处理式子即可 $O(1)$ 求出。

【Scy】D 注意到单组数据，然后看 $455$ 只有 $\binom {15}{3}$ 或 $\binom{15}{12}$ 能凑出来，所以往组合数上靠。转换了一下题意，对于某一行，填的数单调不降；对于某一列，填的数单调不增。然后一下子没什么想法，于是开始尝试凑式子，凑了 $\dbinom {(n + 1)m}{m}$，发现大样例过不了。又想到可以 $\dbinom{n(n - 1) + m}{m}$，然后惊喜地发现对了，于是果断提交过题！

*赛后看讨论，发现第一步的转换正确，在此基础上，每填出一个数，就相当于会对右下角的矩形产生贡献。由于右下角的数不超过 $m$，因此可以进一步转换为放小球问题，在 $n(n - 1)$ 个盒子中放不超过 $m$ 个小球，答案就是 $\dbinom{n(n - 1) + m}{m}$。

【Zlw】中间辗转了好几题，都有点像数据结构。Sky 看了 E 把我喊过来说这题是很明显的数据结构。想了一会没啥明确的思路，不过看到 $10^5$ 的数据范围和非常难维护的 $p$ 映射，大概能猜到是分块。这个时候 Sky 醒说是卡了 $64 \rm MB$ 的空间。这个时候大概能猜到是卡 $O(n\sqrt n)$ 的空间，更加确定是分块。然后能发现整块的贡献与块内 $p\in [l,r]$ 的数量有关，可以直接乘。于是想到可以块内 $p$ 排序然后二分得到，然后散块是区间和单点查，也很好维护。但是此时复杂度 $O(n\sqrt n \log n)$ 并且 $O(\log n)$ 难以塞进根号内部。想到分块平衡复杂度，于是再开一个分块数组实现 $O(\sqrt n)-O(1)$ 的区间加单点查。然后想到上面如果开 $O(n\sqrt n)$ 的前缀和数组也可以做到严格 $O(n\sqrt n)$，调了调块长再把 int 改成 short 发现空间还是留有余地的。于是很快写完。

【Sky & Zlw】Zlw 浅浅看了 B。是个奇妙二分，一开始去算奇怪的限制 WA 了，然后 Sky 说有思路就交给他了。（摆）

观察发现，对于两个数 $s1<s2$，如果进制操作里没有直接转换成一个数（进制但是 $0$ 次方）的话，相当于是只有加法乘法操作，得到的答案肯定有 $s1^\prime<s2^\prime$，如果有直接转换成一个数的话，得到的就是 $s1^\prime=s2^\prime$，整合起来就是 $s1^\prime\leq s2^\prime$，当然这里前提都是合法进制转换。

直接考虑从$[2,M]$二分答案，对于一个 $mid$，只需要直接模拟它能不能完成进制转换即可。我们可以先二分一个结果不小于 $y$ 的答案，然后再二分第一个结果大于 $y$ 的 $ans_r$，那么答案就是 $ans_l$，$ans_r - 1$。时间复杂度 $O(\log M \sum l_i)$。

题目真的不难，但比赛前期中期根本没人做这题，榜都不知道歪到哪里去了，直到最后一小时才发现过这道题的人越来越多，但最后时间不够没有调出来。

【Scyの补题】

G 题没往 dp 上想。设 $dp_i$ 来表示 $\texttt{L}$ 的复位时间，再设 $g_i$ 表示 $[1,i]$ 中 $\texttt{R}$ 的个数。由于 $\texttt{LL…}$ 的情况会造成排队效应，于是有表达式 $dp_i = \max (dp_{i - 1},g_i)$。不难想到可以用 ddp 来维护 $\max+$ 矩阵。

具体来说，若当前为 $\texttt{L}$，则矩阵可以描述为

若当前为 $\texttt{R}$，则矩阵可以描述为

最后的时间复杂度为 $O(n + q \log n)$。

【省流版】

$5/10$ 题，$\texttt{rank 224/1501}$，下分了 qwq。

【Scy】发现 C 是签到，发现只要维护当前最大值与元素差之和即可，直接开写，一发通过。

【Scy】继续看了 F，没啥想法。猜了个每次减去 $\lfloor\frac{\text{average}}{n}\rfloor$ 的暴力发现最后 $0$ 和 $1$ 出现的异常多，但是此时还没想到结论。这时候，Zlw 突然点出答案可能就是奇数个数与偶数个数的乘积。

$\texttt{12:39:17}$ 第一发提交，WA！

【Scy】啊呀，忘记开 long long 了！

$\texttt{12:39:44}$ 第二发提交，WA！

【Scy】啊呀，忘记取模了！

$\texttt{12:41:49}$ 第三发提交，AC！

【Scy】我是罪人！呜呜呜呜……

好吧，赛后仔细想了一下，好像还是挺好证明的！

【Sky】G 的题目大意：给定偶数 $n$，构造 $\{1, 2, \cdots, n\}$ 的子集 $S$ 使得大小为 $\frac{n}{2}$ 且 $\forall x, y, z \in S$（可以相等），$xyz$ 不是完全平方数。

观察到完全平方数一定是 $a^{2k}, k \in \mathbb{N}$，那么尝试去构造一些质因数次方和全是奇数的数，这样任选三个乘起来也都是奇数次方，就不会是完全平方数。

考虑先提取所有质数，标记为 $\text{true}$，次方都为 $1$，然后因为题目给了范围是 $2 \leq n \leq 10^6$，可以遍历做 $O(n)$ 算法。记录一个 $\text{ans}$ 动态数组，从 $2$ 开始，如果曾经被标记为 $\text{true}$，直接加入 $\text{ans}$，并将其固定，即至少选这一个质数，剩下的两个数从现有的 $\text{ans}$ 里面随便选（可相同），乘起来并标记为 $\text{true}$，这样就能生成一个质因数次方和全是奇数的数列。

整体理论复杂度是 $O(n^3)$ ，但是 $\text{ans}$ 具有单调性，在遍历过程中可以有乘积 $\geq 10^6$ 直接剪枝，所以最后实际上大概只会跑到 $O(n)$，预处理 $\text{ans}$ 然后输出即可。

Scy 开始以为时间复杂度会爆，但是测了一下跑得异常快，一发 AC！（Scy 在利用 $x^2 \equiv 2 \pmod 3$ 不存在的性质乱搞，还没弄出来就被 Sky 切掉了%%%））

【Zlw】初看 J 想到有效的质因数个数是 $O(\log w)$ 但是比较难分解质因数，于是想到是否可以用破腊肉，于是抄了一个板子，然后修改一下发现 TLE 了，在卡常路上一去不复返。直到某一刻经过 Sky 的提醒，发现貌似可以通过 $\min\{ \frac{\max\{a,c\}}{\gcd(a,c)},\gcd(a,c)\}\leq 10^9$，然后思考是否有分类讨论平衡复杂度的说法。在推式子的过程中发现： $\gcd(x^bG^b,y^dG^d)=G^{d}\gcd(x^bG^{b-d},y^d)$ ，发现 $\gcd(x,y)=1\rightarrow \gcd(x^bG^{b-d},y^d)=\gcd(G^{b-d},y^d)$，于是得到一个可以辗转的式子，试了一下发现可以过，然后又发现由于底数每次都除掉一个大于 1 的数，所以复杂度是 $O(\log w)$，再乘上计算 $\gcd$ 的复杂度总复杂度 $O(T\log^2 w)$ 于是通过。

【Sky & Scy】Sky 先尝试了这道题。A 是一道非常神秘题，Alice 可以旋转 $4 \times 4$ 的矩阵，Bob 则是纯随机。我先写了个暴力想找规律，但是可能角度不太对，因为我发现左上角的 $1$ 在 Alice 旋转无限次数之后到任意一个位置的概率是相等的，那 Alice 难道也是生成的随机矩阵吗？

其实不然。这时候孙✌提醒我，其实是一个条件概率问题，不能单独拿出每一个数来算概率,要找相对关系。

然后 Scy 开始尝试乱搞。想着就是旋转会出现什么性质，使得只有 Alice 的旋转是不会变的。猜了几个东西然后猜到逆序对。考虑到行和列都在变化，所以猜测整一个数组的逆序对。用 Sky 写的暴力输出了一下逆序对的情况，惊讶地发现都是偶数，于是果断写然后提交，通过了！

【Zlw & Scy】尝试推了 I 题，很显然是一个矩阵快速幂的优化题。但是算概率并不是那么容易，Scy 和 Zlw 的式子均没有通过暴力。由于时间不足，最后并没有探出正解。（应该往方案数统计的方向上靠，从而进一步地得到期望）

【省流版】这一周普遍打得都不是很理想，有题目想偏无法拉回导致大方向把控不佳。$5/11$ 题，$\texttt{rank 220/1490}$。

【Zlw】A 是签到题，很简单的枚举，稍微写写细节过了。

【Scy】 C 也是签到，结合物理模型分析，平抛路程的 $x$ 是关于 $H$ 的上凸函数，直接关于对称轴的距离排序即可。

【Scy】他俩在看 J，我先看了 F。首先先预处理出了每一个灯管有哪些数字是亮的，然后对于每一位设状态，看哪些灯管亮起时可以覆盖所有的情况。随便写了一下就过样例，交了以后 WA。手模了几个发现形如 $\texttt{012}$ 与 $\texttt{234}$ 这种数位不能独立去看，因为这组数据只需要一个灯管即可区分，也就是 $2^{7m}$ 的状态，直接状压肯定超时，于是先没有继续写下去。

【Sky】J 题目给了一个 $\sqrt{-2}$ 进制的定义，让你去算两个数在 $\sqrt{-2}$ 进制下的乘法。

考虑到数据范围很大， $\sum{(|A| + |B|)} \leq 2 \times 10^6$ ，即使是简单的乘法也需要 $O(|A| \cdot |B|)$ ，不能再时间范围内通过。

观察到 $A \times B$ 在 $\sqrt{-2}$ 进制下的乘法其实就是：

乘上

快速多项式相乘，考虑 FFT。

现场去找了个板子，乘完之后再做 $\sqrt{-2}$ 进制下的进位处理，简单模拟一下就过了。

题目其实思路不算难，但一开始一直在想不用 FFT 的做法，浪费了些时间，也想不到，就直接上机写了。

【Scy】$\color{red}\large{注意到 \texttt{ Sky } 忘记多组数据清空以及用 \texttt{ memset } 贡献了两发罚时！！！}$

【Zlw】B 很快的发现区间 shift 只有当连段变动的区间长度都是奇数才会翻转奇偶性，但是一开始完全没注意到它的“数据生成”还藏了结论。以为可以硬算逆序对数，陷入了空间陷阱里，测算使用 $24\rm B$ 存一个整数可以把空间压到约 $30\rm MB$，手模了一个实测发现空间在 $\rm [32MB,34MB]$ 波动，非常炸裂。此时浪费了很多时间，才开始去想交换是否也有性质，然后发现只要不是 $i=f_i$ 都会翻转奇偶性，然后写了写过了。$\color{red}\large{浪费了很多时间在非正解卡空间上}$。

【Scy】到很后面才继续思考 F，发现有效的状态似乎并不多，而且答案最大也就是 $7m$。于是尝试剪枝搜索，记录下一个数 $i$ 受到影响的灯管状态 $S_i$，如果要区别两个数字，则最终答案的状态 $T$ 满足 $(T \& (S_i \oplus S_j)) \neq 0$ 即可。另外还加了一个 $S_i \oplus S_j$ 的去重和答案的最优性剪枝。测了一下极限数据，发现跑得很快，提交通过。哎本来第一发提交是 $00:45$，再多思考十几分钟就能通过，现在增加两个多小时的罚时。

【Zlw & Sky & Scy】一开始 Sky 和 Scy 在讨论这道 G。Sky 发现当两点间原来不相连时，贡献为路径上最大值 $-1$，但是 $O(n^2)$ 且没考虑多个最小生成树的清空。Zlw 感觉有点迷，插了一嘴说是可以用 Kruskal 然后加点计数。Scy 认同了我的做法，然后再经过验证没有发现什么问题，于是我上机开写。但是后面发现想要去掉一条无效边的贡献还需要知道这条边最先被删除的时间。我很快有了一个二分+可持久化并查集的想法，但是 $3$ 个 $\log$ 且特别麻烦被 Scy 骂了。发现可以离线，于是提出整体二分，此时 Scy 还没有其它思路，于是我先写了。再结束前 5min 写完，但是有一个地方没有开 long long，还有一个地方没判 $m=0$ 死循环了赛后还调了一年。

赛后 Scy 用另外一个单 $\log$ 算法通过了。就是按照之前的思路 就是先不减去那些原来有的边的贡献，即 $(w_i - 1) \times sz_x \times sz_y$，然后之后按照 Sky 的思路，看原来就有的边 $(u,v)$ 是多算的值，显然就是最小生成树上这条路径的 $\max - 1$。先用 Kruskal 后用树上倍增维护最大值即可。还因为放错倍增位置导致 WA 了很久。

【省流版】继续坠机，G 题 300 多的过题数但是做不出，最后两小时转战 B 但无力回天。以及，榜再次歪，B 题解里写的是 hard。$5/13$ 题，$\texttt{rank 378/1458}$。

【Zlw】M 开局一分钟就有人通过，于是写了个暴力发现 $n>9$ 无解，交上去过了。

【Sky】J 是签到题，读了好几遍才敢写，每行后面加个 nya 即可。猫娘可爱。

【Scy】L 读了会儿题，感觉还是可做的。还没仔细想就被 Zlw 佬叫去一起看 F。F 一看就是 $O(1)$ 结论题，和 Zlw 讨论了一会儿认为要疯狂分类讨论。在草稿纸上画了一会儿，但越分越乱，迟迟无法上机。

之后想着旋转会导致曼哈顿距离的 $|\Delta| = 1$，因此只需要终点两个坐标的 $x,y$ 之和与起点的坐标作差，后取 $\max$ 即可（其实就相当于题解里的旋转操作）。一发 WA，发现忘记开 long long 了，修改后提交通过。

【Zlw & Sky】
Zlw 本来先看了 G 没什么思路，然后 Sky 在看 A，看了一下发现如果要加点，操作数增长的很快。然后画了一下图找了会规律，找到了一个错误的规律（没想着去严谨推，是个败笔），以为是按照根号增长的。然后忐忑的写了一个根号的 dp，交上去 WA 了，又查了好几个样例才发现加点的式子推错了，严谨地写成了 $f_i=f_{i-1}+f_{i-2}+1$，这回正确性没问题了，但是中间有个地方没有把根号层改掉，又罚多了一次时。

具体来说，考虑尽量去构造每个节点的 $|h_{ls_u} - h_{rs_u}| \leq 1$，形成一棵 AVL 树。

观察上面这幅图，可以发现 AVL 树深度为 $1$ 的时候，只需要蓝色一个节点，深度为 $2$ 的时候，需要蓝色和橙色，深度为 $3$ 的时候需要蓝色、橙色和绿色一共 $4$ 个节点。以此类推，我们观察到，AVL 树的深度和所需要的节点有很强的关系。实际上，再想一步就可以得到，想要当前 AVL 树的深度 $h_i$ 加 $1$，我们只需要在这个树的根节点上面加一个节点，新的根节点的另一个子树深度为 $h_i-1$ 即可满足 AVL 树的条件。

这样下来发现其实是近似斐波那契数列，有式子 $f_i = f_{i-1} + f_{i-2} + 1$ 然后再从根节点从上往下跑一个 dp 即可，dp 的部分被 Zlw 佬秒了，但是佬一开始数列搞错了，纠正后 AC。

【Scy & Zlw】拼好题。子序列的 dp，疑似从后面计算日期的数量，然后从前面计算年份的数量。

Zlw 先提出可以先用 $12 \times 31 \times n$ 的时间算出 $[i,n]$ 强制选 $i$ 时合法日期的数量。设 $f_{i,0/1/2/3,M,D}$ 表示考虑 $[i,n]$ 时填月与日中的第 $0/1/2/3$ 位时，月份为 $M$，日期为 $D$，同时强制选 $i$ 时的合法日期数量。最后发现代码在很多细节上出了问题，又调试了好久。

Scy 发现可以用 $O(n)$ 的时间算出 $[1,i]$ 中合法的闰年的数量。主要需要考虑的是被 $100$ 整除的情况。设 $one_{i,j},two_{i,j}$ 表示第 $i$ 位为 $j$，作为年份的千/百位时的数量，均为 $0$ 时注意特判不合法。直接类似前缀和的思想一位一位的推过来，然后计数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
for (int i = 1;i <= n;++i)
{
    pre[i] = pre[i - 1];
    if (!a[i])
    {
        pre[i] = (pre[i] + third) % MOD;
        for (int o = 0;o < 10;++o) third = (third + two[o]) % MOD;
    }
    if (a[i] % 4 == 0)
    {
        two[a[i]] += (one[0] + one[2] + one[4] + one[6] + one[8]) % MOD;
        two[a[i]] %= MOD;
        if (!a[i]) two[a[i]] = (two[a[i]] - one[0] + MOD) % MOD;
    }
    if (a[i] % 4 == 2)
    {
        two[a[i]] += (one[1] + one[3] + one[5] + one[7] + one[9]) % MOD;
        two[a[i]] %= MOD;
    }
    ++one[a[i]];
}

【*】由于 G 三人都无想法，最后遗憾五题离场。本来是可能有时间写别的题的，但是有人不会判断闰年，把暴力代码写错了，于是疯狂对着一份其实早已正确的代码调试，2.5 h 才过了 B。

Sky 有言：

我觉得吧，一道题就应该一个人写，拼好题可以拼思路！
我觉得吧，我们至少先落实一个事情，就是每个人都看一遍每道题，一场比赛至少得把所有题看一遍。
$\tiny\text{我觉得吧，打成这样肯定是因为 Zlw 与 Scy 太依靠 Sky 佬过题了！}$

【Scy の补题】

G 简直为笛卡尔树量身定制。设最后一个删除的数为第 $i$ 个数，则最后剩余区间一定是 $[l,r] (l \le i \le r)$，其中 $r - l + 1$ 即为建立完笛卡尔树后 $i$ 节点的子树大小 $sz_i$。因此，可以留出不超过 $sz_i - 1$ 个位置给区间外的数，每层只可能有 $1$ 个。由插板法可知答案为 $\sum \limits _{k = 0}^{sz_i - 1}\binom{k + dep - 1}{dep - 1}$。

下面来推个式子：

又因为

所以最后第 $i$ 个数作为最后一个数删除的方案数为 $\binom{dep + sz - 1}{dep}$。最后还需要加上全部为空的情况，贡献为 $1$。

【省流版】好消息：两小时不到就五题了！坏消息：五小时以后还是五题！$5/12$ 题，$\texttt{rank 205/1391}$。

【Zlw & Scy】开局 Zlw 写了 D，发现如果连续两位相等必然出现信息丢失，问了下 Scy 和 Sky 说是三次交替异或可以交换。但是一开始忽略了交换两次又换回来了，以为是 $n \bmod 3=1$ 然后答案错误。看了半天没看出问题，叫 fw Scy 过来看看。Scy 想了很久突然发现 Zlw 佬把交换偶数次（相当于又换回来了的情况）也算到答案里了，修改成 $n \bmod 6=4$ 以后通过。

【Zlw & Sky】H 一道简单小题。考虑式子为 a()b=，其中括号里能填 +、-、*，为了得到最短对称，分情况讨论一下即可。很快发现并证明了加法和乘法合法的充要条件是 $a \neq b$。a 和 b 相同的时候一定是 =a()a=，即不合法。不同的时候再考虑 a()b=b()a，长度为 7。但是由于通过率特别低，一直在找反例。中间忍不住交了一发罚时。最后实在没办法暴力枚举减法的所有情况，发现 $a=0$ 存在特例。然后又由于一个低级失误罚了一次时。

【Scy】发现 I 是构造，观察到矩阵性质特别强，每次都需要跳对应的数量。看了题目后外卖到了，于是右手吃饭，左手纸笔迷题，然后就突然发现好像玩出来了。令 $n < m$，从左上角开始，按数字顺序先向下跳，再向上跳，每一列跳满了之后再向左/右跳。试了一下，算法正确，然后猜想无解可能是自然的。Sky 通过同余方程证明出 $\gcd (n,m) = 1$ 时才有解，和我的猜想殊途同归。一发提交后 AC。

【Zlw】比较清秀的数据结构题，Scy 在写构造的时候看了一下，很快发现枚举 $b_2$ 再去维护每个 $b_3$ 的答案就好了，写个线段树过了。

【Scy & Zlw】Zlw 先看了 E，想到 $m = 1$ 时直接贪心归一到最大值即可。然后又提出 $m = 2$ 时是一个最大值，一个其他值。然后 Scy 把这个想法 hack 了，反例是 5 1 1 1 10 1 1，这时候两个数显然为 $5,14$。

想了一会儿，觉得可以直接枚举这两个值，上界在 $2\max\{a_i\}$，然后设 $dp_{i,0/1}$ 表示第 $i$ 个数最后为枚举的前者/后者的值时的最小答案。若前面操作次数不小于当前数字所需的次数，则直接“免费”，总次数变为较小值；否则花费次数为 $\Delta$，总次数为当前值。

Zlw 确认了 Scy 的做法，枚举两个最终值然后 $O(n)$ 跑一遍 DP 就好。由于 Zlw 比较擅长 DP，于是直接甩锅给他来写了，一发 AC。

【Scy】吸取上次的教训，决定题目都看一下，看了 A,C,J。A 是纯大模拟，实现格式化程序的功能。题目超级难懂，大概看了 30 min 才似懂非懂，但是由于细节太多了，迟迟不敢下手，以至于到比赛结束也没写（不过赛时只有 4 个队伍通过了这道题）。C 是搜索+构造题，构造需要花费很长时间，除非爆搜，最后也没写。（主要是想了一会儿一起去看 K 了，如果剩下三小时去写这道题或许能够构造出来。但是这题据说网上也能找到现成的答案，有点迷惑。至于爆搜，直接用哈希的方式来映射这 $60$ 种积木块即可。J 的话也有构造+计算几何的味道，写不了。）

【Zlw & Sky】K 题意有点模糊，考虑先用 Tarjan 缩点，然后再进行一个子树计算合并，式子是 $C = \{x+y, x \in A, y \in B\} \cup A \cup B$。发现缩点完以后还是一棵树，理论上可以直接类树形背包。但是这个时候忘了树形背包的经典结论可以扩展到任意物品重量，一直以为是三次方，甚至开始尝试 bitset 和 NTT，最后还是没卡过去。赛后发现直接做就是对的。

【后记】

  1. 总排名规则：$\color{purple}{单场得分 = 100 \times\frac{解题数}{第一名的解题数}\times \frac{2\times 本场参赛队伍数-2}{本场参赛队伍数+名次-2}}$。
    总排名按分数最高的 5 场之和，参赛不足 5 场的队伍，按所有参赛场次的得分之和计算。
  2. 海外邀请来的选手不计入总排名。

前 $10\%$ 是 $173$ 名，我们 $\texttt{rk }230$，勉强吧！

License

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

Share